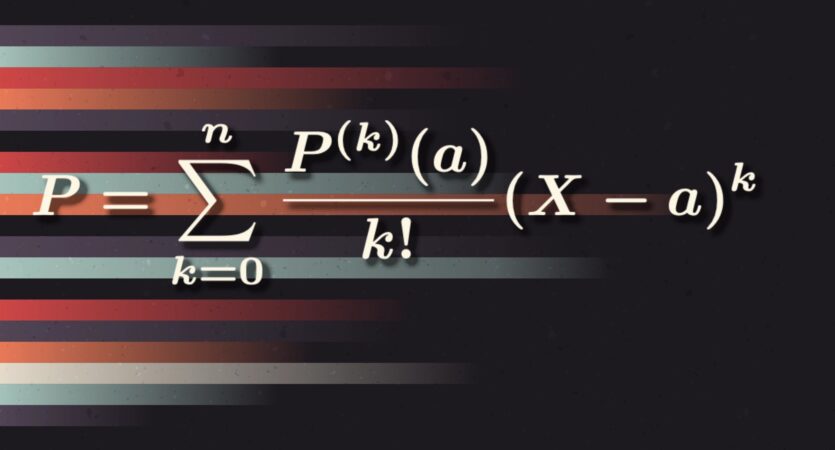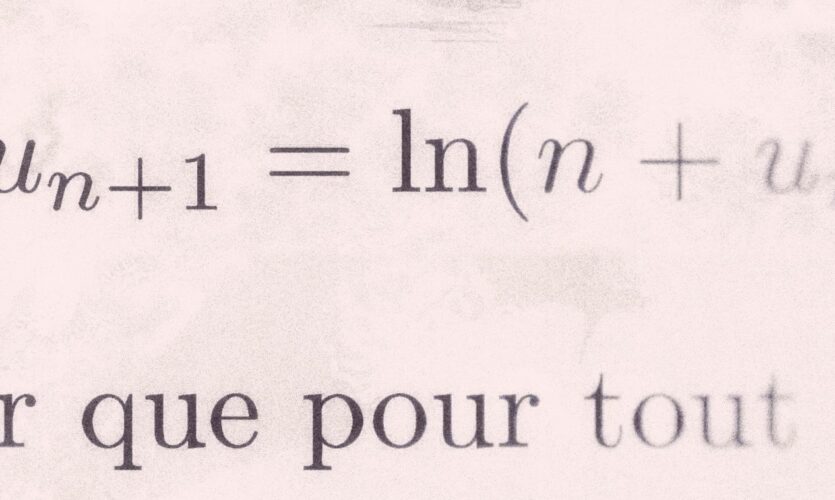Actualités
[Colles de mathématiques] Semaines 19 et 20
Tout sur les fonctions dérivables. Espace vectoriel des polynômes à coefficients dans K. Développements limités et applications.
SAV du DL n°5 de Mathématiques
Le DL n°05 introduit une suite de polynômes dont on étudie quelques propriétés.
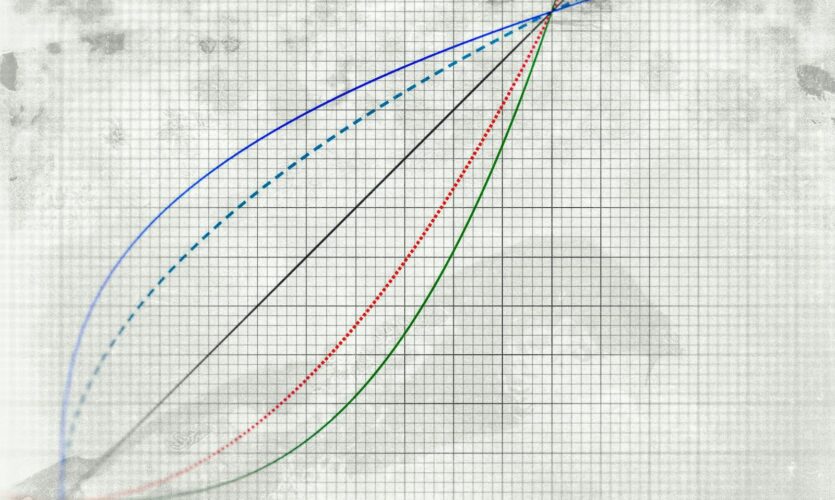
Mouvements dans un champ de force centrale conservatif
La partie « Mouvements dans un champ de force centrale conservatif » est notamment motivée par ses nombreuses applications possibles. On discute…
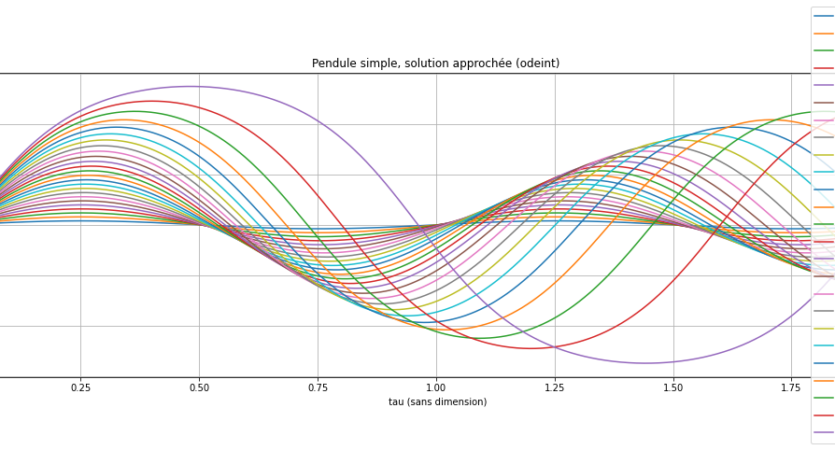
SAV du DM n°4 de Physique
Le DM n°04 porte sur la résolution numérique d'équation différentielles non linéaires du second ordre. Les objectifs sont les suivants : Résoudre…
Moment cinétique
La partie « Moment cinétique » est l’occasion d’introduire les notions de moment cinétique et de moment d’une force. L’un des objectifs…
Exercices de mathématiques
- Tous
- a^x = exp(xln(a))
- Calcul de sommes
- Calcul intégral
- Calculs
- Congruences
- Equations différentielles
- Équivalents
- Études de fonctions
- Fonctions usuelles
- Formules trigonométriques
- Inégalités
- Limites
- Logique
- Nombres complexes
- Polynômes
- Suites
Exercice 10-034 – Limite et équivalents
Calculer une limite d’une forme indéterminée grâce à des équivalents
Exercice 09-023 – Utilisation de la définition de limite d’une suite
Utilisation de la définition de limite d'une suite. Résultat sur une extension du théorème de convergence d'une somme de Cesàro.
Exercice 09-036 – Une suite (presque) définie par récurrence
Suite définie par récurrence, point fixe et vitesse de convergence géométrique.
Exercice 09-042 – Équivalent d’une suite définie pas récurrence
Suite définie par récurrence. Équivalents. Manipulation d'inégalités.
Exercices 07 – CdV : Changements de variable
Lorsqu'il est donné, effectuer un changement de variable dans une intégrale. Comprendre le sens d'application de la formule.
Exercice 06-017 – Une équation différentielle d’ordre 1
EDL d'ordre 1 : utilisation d'une fonction à valeurs complexes pour le calcul d'une primitive.