Actualités
SAV du DM n°3 de Physique
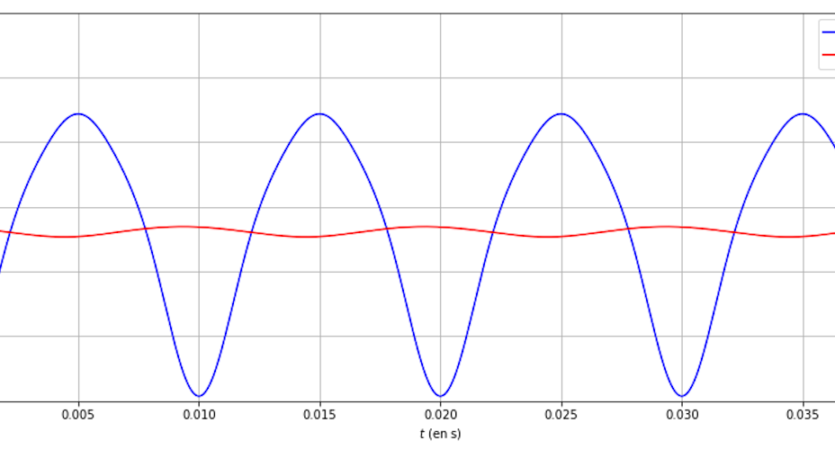
Le DM n°03 porte sur le filtrage linéaire. Les objectifs sont les suivants : Déterminer des caractéristiques d'un signal périodique : valeur…
[Colles de mathématiques] Semaine 12
[mathjax]Calcul intégral dont Intégration par parties et changement de variable. Calcul matriciel : ev \(\mathrm{M}_{np}(\mathbb{K})\), produit de matrices, de matrices triangulaires, transposée.
Propagation d’un signal
Dans la partie consacrée à la « Propagation d’un signal », il est recommandé de s’appuyer sur une approche expérimentale ou sur…
[Colles de mathématiques] Semaine 11
Équations différentielles linéaires d'ordre 1 et 2. Calcul intégral dont IPP et changement de variable. Début du calcul matriciel.
Exercices de mathématiques
- Tous
- a^x = exp(xln(a))
- Calcul de sommes
- Calculs
- Congruences
- Études de fonctions
- Fonctions usuelles
- Formules trigonométriques
- Inégalités
- Logique
- Nombres complexes
- Polynômes
Exercice 05-DERIV
Déterminer le domaine d'étude, de continuité et de dérivabilité d'une fonction usuelle. Calculer une dérivée.
Exercice 03-046
Somme et produit des racines d'un polynôme du second degré. Racines de même module, de même argument.
Exercice 03-058
Définition de module d'un nombre complexe, de partie réelle et imaginaire.
Exercice 01-012 + Indications
La récurrence d'un souvenir, c'est une soudaine, une subite récurrence du passé. Un retour à la mémoire, à la conscience, involontaire et fréquent.
Exercice 00-071 + Indications
Manipuler radicaux et inégalités, étudier une fonction.