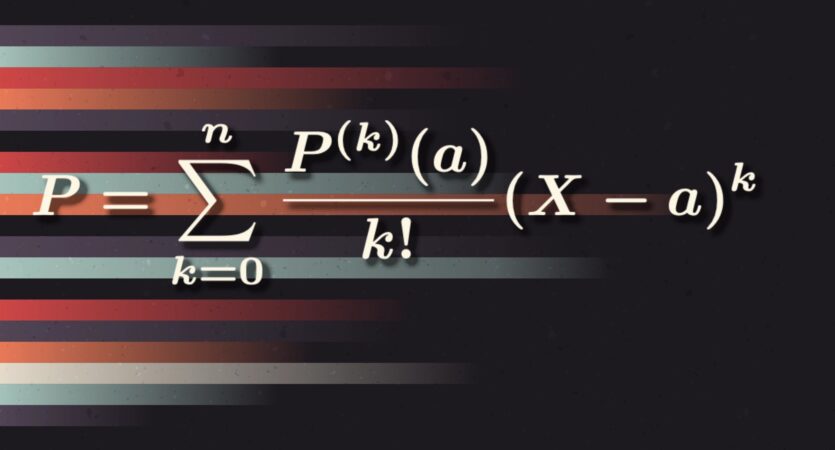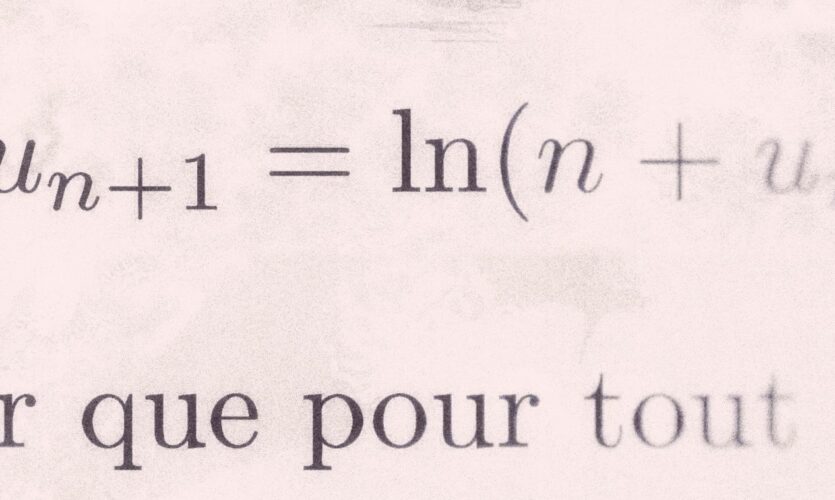Actualités
[Colles de mathématiques] Semaines 21 et 22
Développements limités et applications. Espaces vectoriels et espaces vectoriels de dimension finie. Applications linéaires.
Descriptions microscopique et macroscopique d’un système à l’équilibre
Ce chapitre a pour but de fournir les outils nécessaires à la description d’un système thermodynamique. On expliquera en particulier le passage…
Mouvement d’un solide
Concernant le solide en rotation autour d’un axe fixe dans la partie. « Mouvement d’un solide », il s’agit de définir le…
[Colles de mathématiques] Semaines 19 et 20
Tout sur les fonctions dérivables. Espace vectoriel des polynômes à coefficients dans K. Développements limités et applications.
Exercices de mathématiques
- Tous
- a^x = exp(xln(a))
- Calcul de sommes
- Calcul intégral
- Calculs
- Congruences
- Equations différentielles
- Équivalents
- Études de fonctions
- Fonctions usuelles
- Formules trigonométriques
- Inégalités
- Limites
- Logique
- Nombres complexes
- Polynômes
- Suites
Problème 12-025 – Polynômes de Tchebychev, ou presque !
Construction d'une suite de polynômes vérifiant une certaine propriété
Exercice 10-034 – Limite et équivalents
Calculer une limite d’une forme indéterminée grâce à des équivalents
Exercice 09-023 – Utilisation de la définition de limite d’une suite
Utilisation de la définition de limite d'une suite. Résultat sur une extension du théorème de convergence d'une somme de Cesàro.
Exercice 09-036 – Une suite (presque) définie par récurrence
Suite définie par récurrence, point fixe et vitesse de convergence géométrique.
Exercice 09-042 – Équivalent d’une suite définie pas récurrence
Suite définie par récurrence. Équivalents. Manipulation d'inégalités.
Exercices 07 – CdV : Changements de variable
Lorsqu'il est donné, effectuer un changement de variable dans une intégrale. Comprendre le sens d'application de la formule.