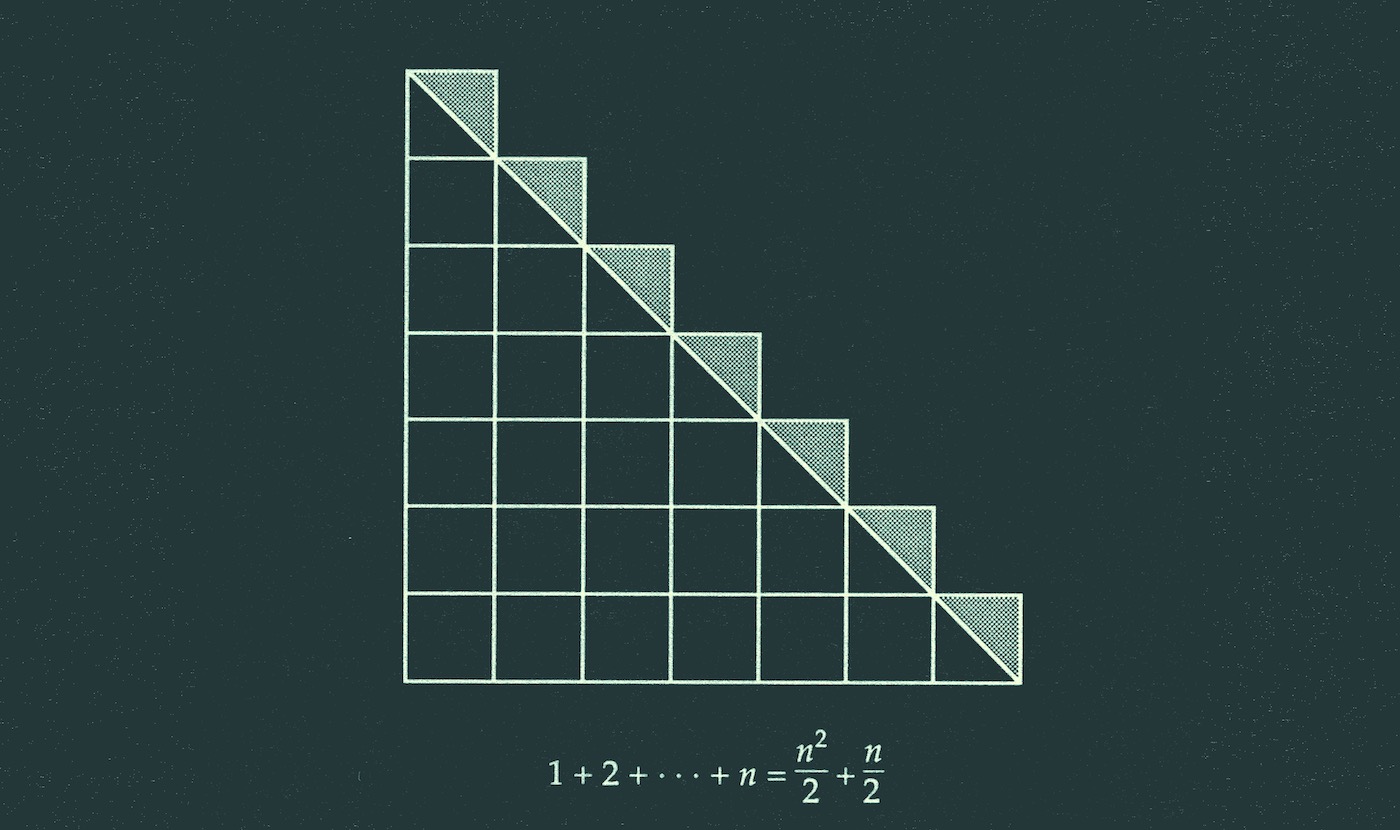
SAV du DL n°2 de Mathématiques
\(\newcommand{\eps}{\varepsilon}
\newcommand{\llbracket}{[\![}
\newcommand{\rrbracket}{]\!]}
\newcommand{\D}{\mathrm{D}}
\newcommand{\C}{\mathbb{C}}
\newcommand{\Q}{\mathbb{Q}}
\newcommand{\R}{\mathbb{R}}
\newcommand{\U}{\mathbb{U}}
\newcommand{\K}{\mathbb{K}}
\newcommand{\N}{\mathbb{N}}
\newcommand{\M}{\mathrm{M}}
\newcommand{\DL}{\mathrm{DL}}
\newcommand{\rg}{\mathrm{rg}\,}
\newcommand{\id}{\mathrm{id}}
\newcommand{\GL}{\mathrm{GL}}
\newcommand{\card}{\mathrm{Card}\,}
\newcommand{\Det}{\mathrm{Det}}
\newcommand{\union}{\cup}
\renewcommand{\Im}{\mathrm{Im}\,}
\renewcommand{\Re}{\mathrm{Re}\,}
\newcommand{\Ker}{\mathrm{Ker}\,}
\newcommand{\vect}{\mathrm{vect}}
\newcommand{\inter}{\cap}
\newcommand{\ch}{\mathrm{ch}\,}
\newcommand{\sh}{\mathrm{sh}\,}
\renewcommand{\th}{\mathrm{th}\,}
\newcommand{\argch}{\mathrm{argch}\,}
\newcommand{\argsh}{\mathrm{argsh}\,}
\newcommand{\argth}{\mathrm{argth}\,}
\newcommand{\Z}{\mathbb{Z}}
\newcommand{\mfrac}[2]{\genfrac{}{}{0pt}{}{#1}{#2}}
\newcommand{\cotan}{\mathrm{cotan}\,}
\newcommand{\tr}{\mathrm{Tr}\,}
\)
Le DL n°02 porte sur les calculs de sommes, les raisonnements par récurrence !
Cet article comporte 14 commentaires
Laisser un commentaire
Vous devez vous connecter pour publier un commentaire.
Bonsoir Monsieur, je ne sais pas par où commencer pour montrer l’hérédité dans l’exercice 1.
Bonsoir Solène. Dans votre récurrence forte, vous supposez que \(x_1=1,\ x_2=2,\ldots,\ x_n=n\). Vous cherchez donc ensuite à montrer que \(x_{n+1}=n+1\).
Vous avez donc UNE inconnue et pas mal d’équations ! En effet, chaque hypothèse sur la suite \((x_k)_{k\in\N}\) est en fait une équation … Mais alors, combien avez-vous d’équations au départ ??
Bref, vous allez travailler sur une équation (une de celles données dans l’énoncé) dans laquelle il n’y aurait que \(x_{n+1}\) comme inconnue (parce que vous connaissez déjà \(x_1,\ldots , x_n\)).
Une fois cette équation identifiée, il n’y aura plus qu’à la résoudre pour trouver \(x_{n+1}\) !
Bonne soirée !
Bonsoir, pour l’exercice 2 je trouve comme résultat : n(n+1)^2 / 2, est ce le bon ? merci
Bonsoir Adam !
Après calcul, j’ai trouvé \(\frac{1}{3}n(n+1)(n+2)\) …. Quelqu’un a le même résultat que moi ?
Dans mon calcul, Adam, je tombe sur du \(\frac{1}{6}n(n+1)(2n+1)\), ce qui explique ensuite mon \(\frac{1}{3}\) !
Bonjour concernant la question 2 du problème 1 , de quelle nature est ak ,est-ce le terme d’une suite ?
Bonjour Clément. Le \(n-\)uplet \((a_1,a_2,\ldots,a_n)\) forme une suite finie d’entiers. La longueur de cette suite (c.-à-d. \(n\)) et les éléments \(a_1,a_2,\ldots,a_n\) qui la composent DÈPENDENT de \(N\) !!!
Par exemple :
– Si \(N=1\) on peut écrire \(N=1=1\times 1!\) donc il existe bien \(n=1\) et \(a_1=1\) tel que \(N=1=a_1\times 1!\)
– Si \(N=2\) on peut écrire \(N=2=1\times 2!+0\times 1!\) donc il existe bien \(n=2\) et \(a_1=0,\ a_2=1\) tel que \(N=2=a_2\times 2!+a_1\times 1!\)
– Si \(N=3\) on peut écrire \(N=3=1\times 2!+1\times 1!\) donc il existe bien \(n=2\) et \(a_1=1,\ a_2=1\) tel que \(N=2=a_2\times 2!+a_1\times 1!\)
– Si \(N=4\) on peut écrire \(N=2\times 2!+0\times 1!\) donc il existe bien \(n=2\) et \(a_1=0,\ a_2=2\) tel que \(N=4=a_2\times 2!+a_1\times 1!\)
– Si \(N=5\) on peut écrire \(N=2\times 2!+1\times 1!\) donc il existe bien \(n=2\) et \(a_1=1,\ a_2=2\) tel que \(N=5=a_2\times 2!+a_1\times 1!\)
MAIS que se passe-t-il ensuite pour \(N=6\) ??
Bon courage !
Bonjour Monsieur,
Pour la question 2 du problème 1, faut-il traduire les indications données comme une proposition et la démontrer dans une récurrence (simple, forte ou double)?
Bonjour Clarisse.
Oui, c’est bien ça, ou presque !
L’unicité ne se démontre pas par récurrence (pas évident en générral).
En revanche, l’existence de \(n\in\N^*\) et de \((a_1,\ldots,a_n)\in\N^n\) vérifiant \(N = cdots\) se démontre par récurrence (simple/faible).
Plus d’infos d’ici 1h … je mange !
Re-Bonjour Clarisse.
Je reviens sur votre question. Regardez aussi ce que j’ai répondu à Clément. Cela va vous aider.
Donc, OUI, vous allez mettre dans un prédicat \(\pi\) certains éléments de l’énoncé pour démontrer, par récurrence simple, que votre proposition \(\pi(N)\) est vraie pour tout \(N\in\N^*\).
Concrètement, pour tout \(N\in\N\), vous poserez \[\pi(N)=\Big(\text{Il existe } n\in\N^* \text{ et il existe des entiers … tel que }N= \cdots \text{ et }a_n\not=0 \Big)\]
Mais on est bien d’accord, ceci ne démontre PAS l’unicité de \(n\) et de \((a_1\ldots, a_n)\) ! Il faut faire un autre raisonnement, et pas une récurrence pour démontrer l’unicité!
Bon courage …
Bonsoir monsieur, pour l’exercice 1, que signifie la question 2 ?
Bonjour Matthieu. Pour moi, il n’y a qu’une seule question dans l’exercice 1 ! Non ??
On sait que pour tout entier \(n\in\N^*,\) \(\sum_{k=1}^nk^3=\big(\frac{n(n+1)}{2}\big)^2=\Big(\sum_{k=1}^nk \Big)^2 \). Autrement dit, il existe une suite \(u=(u_n)_{n\in\N^*}\) de nombres réels strictement positifs vérifiant, pour tout entier \(n\) non nul :\[ \sum_{k=1}^n u_k^3=\Big(\sum_{k=1}^n u_k \Big)^2 \]
Cette suite \(u\), comme on vient de l’expliquer, c’est la suite définie par \[\forall k\in\N,\ u_k=k\]
La (seule et unique) question posée dans cet exercice, c’est celle qui consiste à se demander s’il existerait (oui ou non) une ***autre*** suite \((x_n)_{n\in\N^*}\) de nombres réels strictement positifs vérifiant la même relation, pour TOUT \(n\in\N^*\): \[ \sum_{k=1}^n x_k^3=\Big(\sum_{k=1}^n x_k \Big)^2 \]
……
Et la réponse (donnée dans l’énoncé) est NON ! On doit montrer que si une suite \((x_n)_{n\in\N^*}\) de nombres réels strictement positifs vérifie la relation \[\sum_{k=1}^n x_k^3=\Big(\sum_{k=1}^n x_k \Big)^2 \] pour TOUT \(n\in\N^*\), alors FORCÉMENT, la suite \((x_n)_{n\in\N^*}\) EST la suite \(u=(u_n)_{n\in\N^*}\); autrement dit, pour TOUT \(k\in\N^*,\ x_k=k\) !
Indication : faire une récurrence forte !
Bon courage …
Bonjour Monsieur, pour l’exercice 1 nous avons un début et nous voulons savoir si nous sommes sur la bonne voie.
Merci.
Bonjour. Ce que vous avez écrit est juste, mais je ne vois pas comment vous pouvez vous en servir pour répondre à la question posée dans l’exercice …
En fait, il s’agit d’un exercice sur les récurrences. Il n’y a pas tellement de calcul de somme. Posez une proposition : pour tout \(k\in\N^*\), on note : \[\pi(k)=\Big( x_k=k \Big)\]
L’énoncé vous dit qu’on suppose que pour tout \(n\in\N^*,\ \sum_{k=1}^n x_k^3=\Big( \sum_{k=1}^n x_k \Big)^2\). Sachant cela pour TOUT \(n\in\N^*\), initialisez votre récurrence en montrant que \(\pi(1)\) est vraie c.-à-d. \(x_1=1\).
Indication : vous devrez faire une récurrence FORTE. courage …